С. А. Нефедов, П. В. Турчин

ОПЫТ МОДЕЛИРОВАНИЯ ДЕМОГРАФИЧЕСКИ-СТРУКТУРНЫХ ЦИКЛОВ

Опубликовано в альманахе «История и математика». 2006. №2.

Как утверждает неомальтузианская теория, развитая в работах М. Постана, В. Абеля, Э. Ле Руа Ладури, Ф. Броделя, П. Губера (Abel 1935; Le Roy Ladurie 1966;Goubert 1960; Braudel 1986; Postan 1973) и других авторов, в традиционных обществах ограниченность ресурсов периодически приводит к перенаселению и кризисам, принимающим масштабы демографических катастроф. Таким образом, динамика населения носит циклический характер, и исторический процесс складывается из так называемых демографических циклов. В последнее годы изучение демографических циклов проводится с широким использованием экономико-математических моделей. Это новое направление исследования представлено, в том числе, в работах Дж. Комлоса, А. В. Коротаева, Д. А. Халтуриной, С. Ю. и А. С. Малковых, С. В. Циреля, а также в работах авторов (Komlos, Nefedov 2002; Korotaev, Khaltourina 2006. Коротаев, Малков, Халтурина 2005; Nefedov 2003; Tsirel 2005; Turchin 2003).

В работах Дж. Голдстоуна (Goldstone 1991), в частности, было показано, что кризис в конце цикла вызывался комплексными причинами – не только непосредственно перенаселением, которое приводило к крестьянским восстаниям, но и финансовым кризисом государства, который, в свою очередь, приводил к мятежам военной элиты и общему разрушению общественного порядка. В одной из работ авторов была предложена простая модель, отображающая механизм демографически-структурного цикла в первом приближении (Нефедов, Турчин 2006). В настоящей статье мы предлагаем для обсуждения более развернутую модель, отображающую этот механизм с большей степенью подробности.

Для удобства мы будем рассматривать не календарные, а хозяйственные годы, которые начинаются со сбора урожая. Первоначально в рассмотрение берется только численность простого народа, численность элиты, получающей средства за счет налогов (или ренты) не учитывается. Численность народа (N), выражается в числе дворов или семей (условно можно считать населенность двора в 5 человек). Крестьянский двор, в теории (то есть, когда хватает земли), обрабатывает стандартный участок земли (такой участок назывался на Ближнем Востоке «чифт»), и максимально возможную площадь пахотных земель мы будем измерять числом стандартных участков S. Когда численность дворов N превосходит S, на некоторых участках может разместиться два двора или часть семей может переселиться в города и зарабатывать на жизнь ремеслом, обменивая свои изделия на крестьянские излишки.

Пусть а – урожайность, выраженная числом минимальных семейных пайков зерна, которые можно собрать со стандартного участка. Норма потребления зависит от климатических условий, например, для Малой Азии и Балкан исследователи принимают норму душевого потребления примерно в 200 кг (Lefort 2002: 301), для России с ее суровым климатом – 15 пудов, то есть около 240 кг (Шапиро 1971: 50)). Стандартный участок, «чифт», в Малой Азии в XVI веке давал около 2000 кг чистого сбора (Сванидзе 1990: 266), то есть урожайность а была примерно равна двум, и «чифт», в отсутствие налогов, мог прокормить две семьи. На новгородчине (в Водской пятине) в середине XVI века двор (средним размером в 5,3 души) получал со стандартного участка («обжи») 154-175 пудов хлеба (Нефедов 2005: 48), что давало урожайность (а) в пределах 1,9-2,2.

Урожайность не является постоянной величиной, поэтому мы зададим ее в виде a=a₀+d, где a₀ – средняя урожайность, d – случайная величина, принимающая значения на отрезке (-а₁, а₁). Примерно оценить величину разброса урожайности (а₁) можно, обратившись к российской урожайной статистике. За период 1850-1909 гг. отношение урожая текущего года к среднему десятилетнему варьировало в пределах от 0,62 до1,3 (Загайтов, Половинкин 1984: 235-236), то есть отношение v_a =а₁/a₀ составляло примерно 0,4 (если a₀ =2, то а₁=0,8). Распределение отклонений на отрезке (0,62; 1,3), конечно, не было равномерным. Урожай в пределах от 0,6 до 0,8 среднего наблюдался в течение 9 лет из 60, то есть вероятность низкого урожая составляло примерно 15%. Если в качестве случайной величины взять квадрат равномерного распределения на отрезке (0,6; 1,4), то вероятность низкого урожая составит 12,5%, что примерно соответствует российскому случаю.

Разумеется, в некоторых случаях отношение v_a могло быть больше или меньше 0,4. Например, для средневекового Египта разброс урожайности составлял 60% к среднему урожаю (Korotaev, Khaltourina 2006: 66).

При принятых нами единицах измерения урожай Y можно выразить в простой форме:

Y=aN если N<S,

Y=aS eсли N>S.

С урожая берется налог в m процентов, и после его вычета у крестьян остается (1-m)Y пайков, и на семью приходится p₁ = (1-m)Y/N пайков. Если имеются излишки, то есть p₁ больше некоторой величины «удовлетворительного потребления» p₂ (p₂>1), то крестьяне потребляют не все это зерно, откладывая p_n процентов в запас, то есть потребление p равно

p=p₁(1- p_n) если p₁>p₂

В расчетах обычно берется p₂ =1,2 и p_n =0,05, а при р₁ больше 1,4 p_n =0,1 , то есть крестьяне откладывают при среднем урожае 5%, а при большом - 10% урожая. Нужно отметить, однако, что в силу условий хранения крестьянские запасы не могут увеличиваться до бесконечности, и ограничены некоторой величиной F_p. В расчетах принимается F_p = 4, то есть крестьяне могут хранить запас в 4 годовых пайка для каждого члена семьи.

Если потребление падает ниже уровня p₃, (в расчетах p₃=1,1) то крестьяне берут зерно из запасов, поднимая, по возможности, потребление до уровня p₃. Если же крестьянские запасы иссякают и в годы голода потребление оказывается меньше нормы (p₁<1), то государство, в некоторых случаях, помогает крестьянам из своих запасов. Однако в силу инертности государство оказывает помощь, когда голод уже начался, и потребление при этом поддерживается на уровне p_1k, меньшем единицы (т. е. минимальной нормы). Однако создание государственных амбаров для помощи крестьянам практиковалось не во всех странах; во многих случаях крестьянам приходилось рассчитывать на собственные силы (p_1k=0).

Коэффициент роста населения r есть отношение населения последующего года к населению предыдущего года. Коэффициент роста r зависит от потребления. Когда потребление равно минимальной норме (p=1), население остается постоянным (r=1). Максимальный естественный рост обозначим r_m, а величину потребления, при которой он достигается – p_m. Мы полагаем r_m =1,02, то есть максимальное увеличение численности населения составляет 2% в год. Мы будем считать, что при 1<p<p_m рост населения линейно зависит от потребления, а при p>p_m уже не увеличивается (r=r_m). При p<1 (в случае голода) зависимость r от p берется в форме r=p^k, где k – некоторый коэффициент. В данном случае имеет место сокращение населения, причем не только из-за голода, но и по причине распространения эпидемий, вызванных ослаблением сопротивляемости организма в результате голодовок. Если брать коэффициент k равным единице, то получится, что число выживших равно числу наличных минимальных пищевых норм. На практике, однако, известно, что люди выживали и при недостаточном питании, поэтому в наших расчетах обычно берется k =1/4; при таком значении параметра при падении потребления наполовину погибает 16% населения.

Доходы государства в обычное время равны m процентов от урожая, причем мы считаем, что в налоги входит и рента, которая в государствах Востока была той частью налога, которая шла воину, получившему поместье. В годы кризиса налоги не могут собираться полностью, в этом случае они уменьшаются в соответствии с величиной коэффициента стабильности k_p предыдущего года (см. ниже) и равны k_pm. В принципе, ставка налогов m может меняться, и мы рассмотрим этот вопрос в дальнейшем.

При распределении поступлений от налогов основная часть достается военной элите, а запасы формируются из оставшихся сумм. При численности войска N_f и норме содержания воина p_f, войско требует расходов E= N_f p_f. Если доходы, равные S= mY, превосходят расходы, то k_d процентов от излишка d_s= S-E откладывается в запас, а остальная часть расходуется на увеличение войска. Если же расходы превосходят доходы, то необходимые средства берутся из запаса; если казна пуста, то содержание каждого воина уменьшается и реально равно p_r= S/N_f. При уменьшении содержания постепенно уменьшается и численность войска, она зависит от величины p_g среднего содержания за n_g лет и равна N_f = ₍p_g/p_f)^ksN_f-1, где k_s – некоторый коэффициент, который характеризует способность государства сокращать армию. Если содержание падает наполовину, то при k_s=0,2 армия сокращается в год на 13%, если же k_s=0,02, то только на 2,5%. Последний случай соответствует ситуации феодального войска, которое представляет собой вассалов короля; вассалов нельзя уволить со службы, и сокращение такой элиты возможно только в результате внутренней войны. Срок, для которого рассчитывается среднее содержание, принимается равным десяти годам.

Уменьшение содержания военной элиты вызывает смуты. Интенсивность смут измеряется коэффициентом государственной стабильности k_g, который зависит от средней величины содержания p_g и имеет вид

k_g=( p_g/p_f )^u(k_g-1)^v(k_p)^w

Коэффициент k_g меняется от 0 (хаос) до 1 (полная стабильность) и зависит также от величины стабильности в предыдущий год k_g-1 и от стабильности среди простого народа k_p. Величины u, v и w в этой формуле – степени порядка 0,1-0,3; их значение состоит в том, чтобы амортизировать влияние p_g , k_g-1 и k_p. Если финансовый кризис ликвидирован, то при v =1/4 коэффициент стабильности за три года возрастает с 0,5 до 0,99. При w = 0,1 нестабильность в народе уровня 0,8 вызывает нестабильность в элите уровня 0,97, то есть крупное крестьянское восстание порождает небольшие военные мятежи. Величина u в расчетах принимается равной 1/4; при этом значении параметра половинное сокращение содержания вызывает нестабильность порядка 0,84. При этом (как и при определении периода среднего содержания) мы исходим из того обстоятельства, что воины, в отличие от крестьян, при сокращении содержания не голодают и поэтому могут выдерживать такое положение долгое время.

В конечном счете, политическая нестабильность приводит к нарушению хозяйственной деятельности, к падению урожайности и сокращению посевных площадей. Мы будем условно считать, что стандартные крестьянские участки остаются прежними, включая эффект их сокращения в общее падение урожайности. Величина падения урожайности зависит от коэффициента k_g.

Другой источник нестабильности – это голод, который приводит к крестьянским восстаниям и нарушению обычного хода хозяйственной жизни, например, по причине отсутствия зерна для посева. В конечном счете, эти факторы также ведут к падению урожаев. Коэффициент уменьшения урожайности из-за голода и крестьянских восстаний зависит от средней величины потребления (p_np) за несколько (n_p) лет, причем величина потребления за последний год входит в это усреднение с двойным весом. Мы будем считать, что эта зависимость степенная и имеет вид k_p = (p_np)^l(k_g)^v(k_p-1)^w где l – некоторый параметр. В расчетах обычно берется среднее потребление за два года, а l=3, то есть население достаточно эмоционально реагирует на голод. Коэффициент k_p является также мерой стабильности в среде простого народа, он меняется от 0 до 1 и зависит от стабильности в предыдущий год k_p-1 и стабильности в среде элиты k_g .

Общее падение урожаев из-за политической нестабильности дается коэффициентом k_gp= k_gk_p, однако в любом случае урожайность не может упасть до нуля, поэтому мы ограничиваем величину этого падения коэффициентом k_gp0. Какова может быть величина k_gp0? Сведений об урожаях в годы кризисов немного, но известно, например, что урожай 1922 года в СССР был на 32% меньше, чем средний урожай 1925-1929 годов (Социалистическое строительство СССР 1934: 203). Собственно урожайность при этом уменьшилась незначительно (на 3,8%), но сильно сократились посевные площади (Социалистическое строительство СССР 1934: 176-177) что позволяет утверждать, что падение урожаев было, в основном, результатом предшествующего политического кризиса. Мы будем ориентировочно считать, что средняя урожайность a₀ (куда в нашем случае входит и уменьшение посевных площадей) в годы кризисов может максимально сократиться на треть.

Мятежи военной элиты и крестьянские восстания приводят не только к разрушению хозяйства, но и непосредственно к гибели участвующего в конфликте населения. Мы будем полагать, что процент населения, ставшего жертвой конфликта, выражается формулой M_n= l_g(1-k_g)+ l_p(1-k_p) , где l_g и l_p – некоторые параметры. В расчетах обычно принимается l_g=0,01 и l_p=0,02, что может приводить к ежегодному уменьшению населения в годы кризиса на 2%.

В реальной истории, хотя налоги формально фиксировались, они имели скрытую тенденцию к повышению: побуждаемое финансовым кризисом правительство было вынуждено вводить различные «чрезвычайные» сборы, или владельцы поместий требовали с крестьян «незаконные» надбавки. Этот процесс непосредственно стимулировался военными мятежами, когда разбухшее войско протестовало против сокращения своего содержания. С другой стороны, крестьянские восстания в ходе глобальных кризисов заставляли государство снижать налоги; таким образом, величина налогов, в конечном счете, определялась тем двусторонним давлением, которое оказывали на государство военная элита и народ, и которое в нашей модели выражается, соответственно, коэффициентами стабильности k_g и k_p. Мы будем полагать, что уровень налогов m_l определяется по формуле

m_l = m_l-1 k_p /(k_g)^s

где m_l-1 – уровень налогов предыдущего года и s - некоторый параметр. Если ситуация стабильна, то k_g= k_p=1 и уровень налогов не меняется. Военные мятежи (k_g<1) заставляют правительство повышать налоги; восстания (k_p<1) приводят к уменьшению налогов. В периоды кризисов, когда оба коэффициента меньше 1, ситуация определяется взаимным соотношением k_g и k_p, для регулирования которого используется параметр s. s выбирается так, чтобы силы народа и элиты были сбалансированы и средняя величина налогов не менялась значительно от цикла к циклу – то есть нашей целью является рассмотрение относительно стабильных систем, не эволюционирующих в социальном отношении. При этом предполагается, что налоги не могут быть снижены ниже некоторой величины m₁, определяемой потребностями обороны государства и не могут быть повышены выше величины m₂, определяемой платежноспособностью крестьянина. В наших расчетах m₁=0,1, m₂=0,4.

Перейдем к описанию численных экспериментов. Как отмечалось выше, нашей главной целью было изучение изменения динамики населения и хода кризиса в зависимости от влияния различных параметров. В наших расчетах мы условно брали площадь пахотных земель S в 1 млн. стандартных крестьянских участков. Средняя урожайность a₀ =2, то есть в отсутствии перенаселения одна крестьянская семья в среднем имела чистый сбор зерна в два минимальных пайка. Разброс урожая составлял от 1,2 до 2,8, а случайная величина разброса была квадратом равномерного распределения. Величина государственных запасов ограничена годовым пайком минимальным пайком на семью; максимальное потребление крестьян p_m =2,5 минимальной нормы. Норма потребления на элитную семью составляла восемь минимальных крестьянских норм. Начальная численность для простого народа берется в 0,9 млн. дворов.

Известно, что в Османской империи в XVI веке налоги составляли 1/6-1/5 урожая (Inalcik 1993: 71). Мы возьмем первоначальный уровень налогов в 20% и будем полагать, что государство (как Османская империя) является достаточно сильным: оно способно отчислять в резерв 90% (k_d =0,9) от профицита бюджета, и в случае необходимости сокращать армию на 13% в год (k_s=0,2). В Османской империи, в Китае и в некоторых других странах существовала система государственных зерновых складов, из которых население могло в случае голода получать продовольственные ссуды (Inalcik 1993: 98; Lee 1921: 350). Рассмотрим сначала случай, когда при голоде государство оказывает помощь крестьянам, поднимая величину потребления до 0,99 минимальной нормы. Так как в расчетах присутствует случайная величина, урожайность, то при различных прогонах программы результаты расчетов могут различаться, но в целом получается достаточно типичная картина.

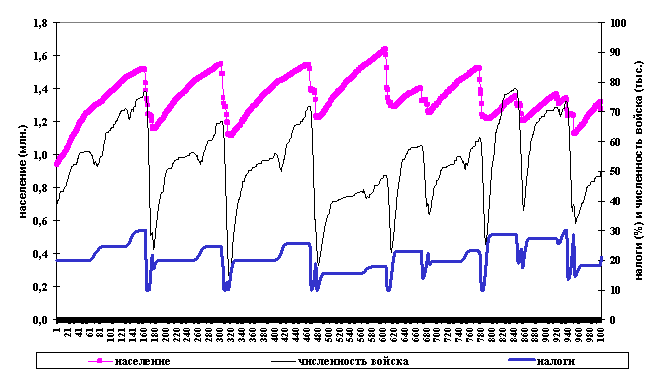
Рис. 1. Динамика численности населения в млн. дворов. Вариант расчета с первоначальным уровнем налогов в 20%, k_d =0,9, k_s=0,2, s=0,6.

Как видно из рис. 1, при данных значениях параметров наиболее типичными являются циклы продолжительностью примерно в полтора столетия, демографическая катастрофа происходит при приближении к потолку населения в 1,6 млн., и численность населения падает до 1,1-1,2 млн.

Как отмечалось выше, в этом и во всех последующих случаях параметр s подбирается так, чтобы средние налоги на протяжении циклов были примерно одинаковы. Тем не менее, они могут варьировать в определенных пределах. Как видно из рис. 1 на протяжении цикла налоги, как правило, растут: время от времени казна оказывается пустой и вынуждена уменьшать содержание войска, что сопровождается его сокращением. Недовольная военная элита поднимает мятежи, и в итоге, правительство вынуждено увеличивать налоги – ситуация, многократно наблюдавшаяся в истории разных стран. Те циклы, в которых уровень налогов ниже, имеют большую продолжительность и больший потолок населения; если же налоги выше среднего уровня, то циклы, соответственно, становятся короче, а потолок населения – ниже. Численность элиты пропорциональна величине налогов (ренты), и особенно велика в коротких циклах: причиной малой продолжительности этих циклов является чрезмерное давление элиты на народ. П. Турчин обратил внимание на то обстоятельство, что в средневековой истории Северной Африки преобладали именно такие короткие циклы – циклы ибн Халдуна (Turchin 2003). Недавно А. В. Коротаев и Д. А. Халтурина предложили математическую модель этого явления, а так же заметили, что население в то время не достигало потолка емкости среды (Korotaev, Khaltourina 2006: 47). Как нам представляется, эта специфика может быть объяснена из предлагаемой нами модели, если учитывать существовавший в этой стране высокий уровень налогов.

В конечном счете, перенаселение в условиях роста налогов приводит к кризису, механизм которого более подробно изображен на рис. 2.

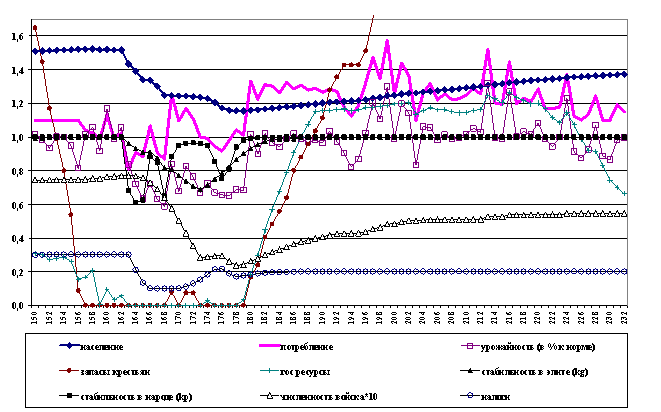
Рис. 2. Механизм демо-популяционного кризиса.

Как видно из рис. 2, в 150-х годах крестьяне жили в условиях перенаселения, им приходилось использовать зерно из своих запасов, и эти запасы быстро уменьшались. В 157 году запасы иссякли, и крестьяне стали обращаться за поддержкой к государству, но государственных запасов хватило ненадолго, к 163 году они закончились. В этих условиях большой неурожай 163 года сразу же вызвал голод и крестьянское восстание. Это негативно повлияло на хозяйственную жизнь и в следующем, 164 году, снова был большой неурожай, который усилил голод и восстания. С другой стороны, недобор налогов вызвал сокращение содержания войска и стимулировал военные мятежи. К 169 году население значительно сократилось, а налоги уменьшились вдвое, поэтому (хотя из-за гражданской войны урожаи оставались плохими) душевое потребление увеличилось и превысило норму. Восстания почти прекратились, но из-за уменьшения налогов и сокращения населения доходы военной элиты резко уменьшились, и она продолжала бунтовать. Внутренняя война привела к новому голоду и новой вспышке восстаний в 173-177 годах, но, в конечном счете, численность военной элиты сократилась и государству стало легче ее содержать. С другой стороны, военные мятежи убедили правителей в необходимости восстановить налоговую систему и увеличить налоги. (хотя они не достигли прежнего уровня). В 180 году у крестьян и казны появились небольшие запасы; вскоре после этого военные мятежи закончились.

В описанной модели кризиса главным моментом является перенаселение, которое вызывает сначала истощение запасов крестьян, а потом – запасов государства. В этой ситуации неурожаи вызывают крестьянскую войну, а финансовый кризис провоцирует военные мятежи.

Рассмотрим теперь вопрос о том, какие изменения в динамике населения могут произойти при вариации различных параметров. Увеличим первоначальный налог до 30% урожая. Демографическая динамика, моделируемая в этом случае, изображена на рис. 3. Расчеты показывают, что потолок населения и среднее население (за 1000 лет) снизились, уменьшились средние крестьянские запасы, но возросли государственные запасы и численность войска. Немного понизилось среднее потребление, циклы стали более короткими, а их амплитуда уменьшилась. Эти тенденции сохраняются и при дальнейшем увеличении налогов. При 40-процентных налогах (рис. 4) можно говорить о некоей квазистабильности: кризисы становятся менее заметными и уносят порядка 10 % населения. В то же время уменьшение крестьянских запасов приводит к тому, что крестьяне часто испытывают нехватку зерна и обращаются к помощи государства даже на ранних стадиях цикла. Вследствие этого кривая населения становится неровной, вибрирующей.

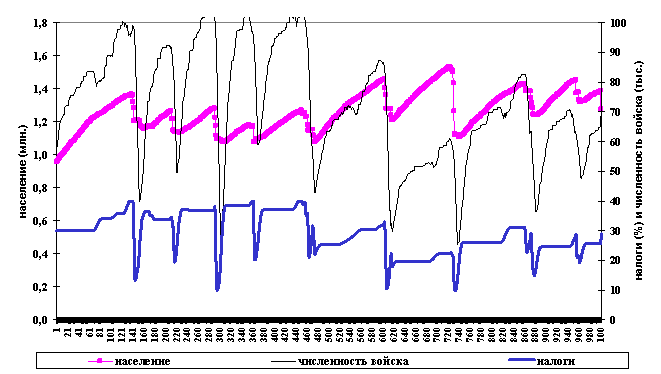
Рис.3. Вариант расчета с первоначальным уровнем налогов в 30%, k_d =0,9, k_s=0,2, s=0,55.

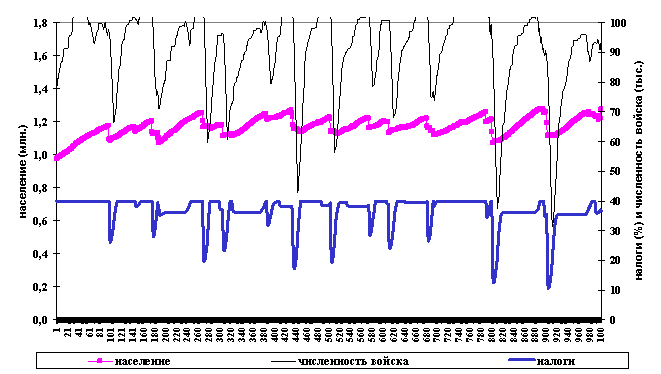
Рис.4. Вариант расчета с первоначальным уровнем налогов в 40%, k_d =0,9, k_s=0,2, s=0,55.

Этот результат – относительная стабильность при повышении налогов кажется парадоксальным. Однако необходимо отметить, что он достижим только в условиях сильного государства, которое может отчислять в резерв 90% излишка и сокращать военную элиту, попросту распуская наемное войско.

Если же государство слабеет, то картина меняется. Это проявляется, прежде всего, в том, что элита требует большей доли налогов (ренты) и в невозможности быстро сократить войска. Как показывают расчеты, увеличение доли элиты и сокращение отчислений в резерв приводит к тому, что казна не имеет значительных ресурсов для того, чтобы обеспечить стабильное снабжение войска, военная элита постоянно поднимает мятежи, в результате чего налоги (рента) быстро увеличиваются. При этом картина коротких циклов с малой амплитудой сохраняется.

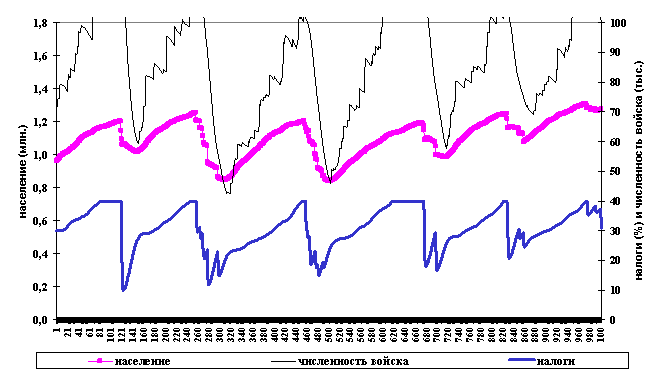
Рис.5. Вариант расчета с первоначальным уровнем налогов в 30%. k_d =0,9, k_s=0,02, s=0,2.

Картина меняется, если государство слабеет настолько, что не может свободно сокращать войска, то есть они принимают отчасти феодальный характер. В случае, изображенном на рис. 5 k_s=0,02, и при понижении содержания наполовину от нормы военная элита уменьшается за год только на 2,5%. На рис. 6 более подробно представлен механизм кризиса, реализуемый моделью в данном случае. Из графика видно, что период перед кризисом характеризовался хроническим отсутствием государственных ресурсов, следствием чего были постоянные мятежи знати, с успехом добивавшейся увеличения ренты-налога. Мятежи привели к уменьшению урожаев и быстрому исчерпанию крестьянских запасов, еще до того, как экологическая ниша была заполнена. В 456 году начался голод, следствием которого были крестьянские восстания. Восстания привели к уменьшению ренты, что еще более ухудшило положение элиты и отдельные мятежи переросли в гражданскую войну. Поскольку численность элиты снижалась очень медленно, то внутренние войны затянулись на 70 лет; потери в войнах уменьшали численность населения, поэтому оно не росло. Этот период – так называемый «интерцикл» или фаза депрессии - может быть и более длительным; он наблюдался в реальной истории многих европейских стран. В работах П. Турчина показано, что интерцикл порождается ситуацией политической нестабильности, то есть внутренними войнами и усобицами, которые препятствуют росту населения (Turchin 2005, 2006).

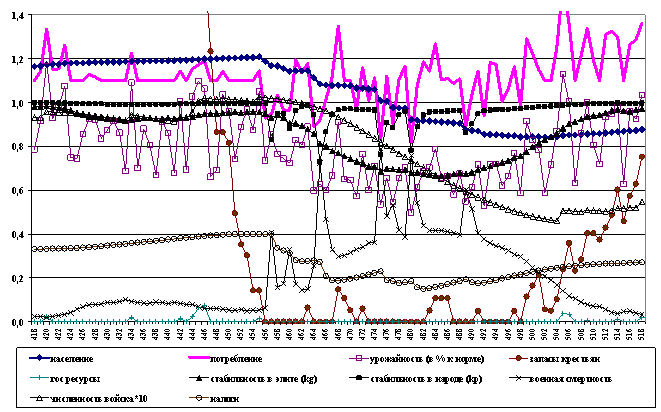
Рис. 6. Элитно-популяционный кризис и интерцикл.

Описанный выше тип кризиса отличается от рассмотренного ранее (рис. 2) тем, что элитные мятежи вызывают разрушение хозяйства и голод приходит еще до момента реального заполнения экологической ниши. Тем не менее, и в этом случае главной причиной кризиса является рост населения, который приводит к уменьшению крестьянских наделов и к тому, что крестьяне не могут обеспечить ресурсами войско. Таким образом, мы имеет два типа кризисов, в первом из которых инициирующую роль играет народ, а во втором – военная элита, и которые можно назвать соответственно «демо-популяционнным» и «элитно-популяционным». В реальной истории эти два типа кризисов встречаются достаточно часто. Демо-популяционный характер имело большинство китайских кризисов, в частности, «восстание красных бровей», «восстание желтых повязок», восстание Ли Цзы-чена, восстание Хуан Чао, восстание тайпинов. Элитно-популяционный характер имел кризис, связанный с мятежом Ань Лу-шаня, османский кризис 1595-1605 годов (восстание Кара Языджи), кризис Империи Великих Моголов в 1710-20-х годах.

В случае, когда государство слабо и не может создавать значительные ресурсы, оно не способно оказывать помощь крестьянам, поэтому формальное существование системы для оказания такой помощи не имеет существенного значения. Разница может оказаться существенной только в случае сильного государства, который рассмотрен ранее, но в действительности, она трудно ощутима даже для случая, который изображен на рис. 1 и лишь при детальном рассмотрении удается установить, что при оказании помощи цикл немного продлевается за счет того, что в период перед кризисом крестьяне несколько лет спасаются от голода субсидиями казны (см. рис. 2). При увеличении ресурсов государства такие периоды, естественно, становятся более продолжительными.

Подводя итоги, можно отметить, что как показывает модельный анализ, наиболее стабильными являются государства, создающие большие резервы путем значительных отчислений от налоговых поступлений. Эти отчисления одновременно уменьшают долю элиты в совокупной ренте, и тем самым ее численность. Появляется возможность удовлетворить военное сословие и избежать опасности военных мятежей. Одновременно появляется возможность оказывать помощь крестьянам в случае голода и проводить ирригационные работы. Примеры такой политики дают Япония эпохи Токугава, Египет при тюркских мамлюках (середина XIII-середина XIV века), династии Старшая Хань и Мин в Китае, Османская империя в XV-XVI веках, Византия эпохи Македонской династии. Это – политика сильных автократических государств, держащих в узде военную элиту.

Неспособность аккумулировать средства является оборотной стороной неспособности сдерживать каждодневные финансовые претензии элиты. Это приводит к тому, что государство не может удовлетворить требования войска в годы временных трудностей, что ведет к мятежам военного сословия. Мятежи, в свою очередь, вызывают рост налогов, что влечет голод и восстания. Бесконтрольная раздача икта в империи Сельджукидов в XI веке и в Египте в XII веке привела к резкому росту ренты и демографическим катастрофам.

В целом, эти выводы совпадают с выводами, сделанными нами при анализе поведения модели, описывающей механизм цикла в первом приближении (Нефедов, Турчин 2006: 109).

Проведенный анализ позволил выделить два типа завершающих цикл экосоциальных кризисов и показать их общее происхождение. Это помогает прояснить некоторые спорные вопросы теоретической истории. Например, на протяжении долгого времени среди историков шла полемика о том, какова была природа кризиса 1595-1605 годов в Османской империи (Faroqhi 1993) – был ли это кризис перенаселения или военный мятеж? В данном случае выясняется, что военные мятежи типа восстания Кара Языджи являются одним из вариантов кризисов перенаселения постольку, поскольку «элитно-популяционные» и «демо-популяционные» кризисы описываются одним и тем же алгоритмом.

Литература

Загайтов, И. Б., Половинкин П. Д. 1984. Экономические проблемы повышения устойчивости сельскохозяйственного производства. М.: Статистика.

Коротаев, А. В., Малков, А. С., Халтурина, Д. А. 2005; Законы истории. Математическое моделирование исторических макропроцессов. Демография, экономика, войны. М.: URSS.

Нефедов, С. А. 2005. Демографически-структурный анализ социально-экономической истории России. Екатеринбург: Издат. УГГУ.

Нефедов, С. А., Турчин, П. В. 2006. Модифицированная модель демографически-структурной динамики аграрного общества. Информационный бюллетень ассоциации «История и компьютер». (33): 102-110.

Сванидзе М. Х. Производство зерновых на крестьянском чифтлике (по османским законоположениям в XV-XVI вв.). Османская империя: государственная власть и социально-политическая структура. Ред. С.Ф. Орешкова С. 222-227. М.: Наука, 1990.

Социалистическое строительство СССР. 1934. М.: Союзоргучет.

Шапиро А. Л. 1971. (Ред.) Аграрная история Северо-Запада России. Вторая половина XV-начало XVI века. Л.: Наука.

Abel, W. 1935. Agrarkrisen und Agrarkonjunktur in Mitteleuropa vom 13. bis zum 19. Jahrhundert. Berlin.

Braudel, F. 1986. L' identité de la France. Les hommes et les choses. Paris: Les Editions Artaud,.

Inalcik, H. 1993. The Ottoman State: Economy and Society, 1300-1600. An economic and social history of Ottoman Empire. 1300-1913. /Ed. by H. Inalcik, D. Quataert. pp. 9-410. Cambridge: Cambridge University Press.

Faroqhi, S. 1993. Crisis and Change, 1590-1699. An economic and social history of Ottoman Empire. 1300-1914. /Ed. by H. Inalcik, D. Quataert. pp. 411-436. Cambridge, Cambridge University Press.

Goldstone, J. 1991. Revolution and Rebellion in the Early Modern World. London: University of California Press.

Goubert, P. 1960. Beauvais et le Beauvaisis de 1600 à 1730: contribution à l'histoire sociale de la France du XVIIe siècle. – Paris : S.E.V.P.E.N.

Komlos, J., Nefedov S. 2002. Compact Macromodel of Pre-Industrial Population Growth. Historical Methods. (35): 92-94.

Korotaev, A., Khaltourina D. 2006. Introdaction to social mackrodynamics. Moscow: URSS.

Le Roy Ladurie, E. 1966. Les Paysans de Languedoc. Vol.1-2. Paris : S.E.V.P.E.N.

Lee, Mabel Ping-hua. 1921. The Economic History of China. N. Y.

Nefedov, S. 2003. A model of demographic cycles in a traditional society: the case of Ancient China. Chinese Journal of Population Science. (3): 48-53.

Postan, M. 1973. Essays on medieval agriculture and general problems of medieval economy. London:Cambridge University Pres.

Tsirel, S. V. 2004. On the Possible Reasons for the Hyperexponential Growth of the Earth Population. Mathematical Modeling of Social and Economic Dynamics/ Ed. by M. Dmitriev and A. Petrov, pр. 367–369. Moscow: Russian State Social University.

Turchin, P. 2003. Historical Dynamics. Why States Rise and Fall. Princeton and Oxford: Princeton university press.

Turchin, P. 2005. Dynamical Feedbacks between Population Growth and Sociopolitical Instability in Agrarian States. Structure and Dynamics: eJournal of Anthropological and Related Sciences. (1): 1-19.

Turchin P. 2006. War and Peace and War: The Life Cycles of Imperial Nations. New York: Pi Press.