Нефедов С

Нефедов С. А., Турчин П. В.

МОДИФИЦИРОВАННАЯ МОДЕЛЬ ДЕМОГРАФИЧЕСКИ-СТРУКТУРНОЙ

ДИНАМИКИ АГРАРНОГО ОБЩЕСТВА

Опубликовано в журнале:

Информационный бюллетень ассоциации

«История и компьютер». 2006. № 33. С. 102-110

Завоевавшая большую популярность демографически-структурная теория[1] полагает, что государство является одним из основных факторов, влияющим на поддержание устойчивости экологической ниши и динамику населения. Важная роль государства проявляется в том, что оно пресекает внутренние войны, поддерживает социополитическую стабильность и обеспечивает необходимые условия для производственной деятельности, а также способствует расширению производства, например, путем создания ирригационных систем. Государственную мощь можно сопоставить с объемом находящихся в распоряжении государства финансовых и материальных ресурсов. Однако ограниченность пахотных площадей в аграрных обществах ограничивает доходы государства. С другой стороны, рост населения приводит к росту расходов, вследствие чего появляется бюджетный дефицит и начинается финансовый кризис. В конечном счете государство терпит банкротство, государственная мощь резко падает и государство теряет способность поддерживать порядок. Потеря управляемости в условиях вызванного ростом населения падения потребления и всеобщего недовольства приводит к мятежам знати, народным восстаниям и длительным гражданским войнам. Численность населения сокращается, но душевая обеспеченность землей и потребление увеличиваются, поэтому внутренние войны постепенно стихают, государство восстанавливается и снова начинает оказывать благотворное воздействие на производство—начинается новый «вековой цикл».

Хотя падение численности населения логически можно объяснить как результат смуты, Дж. Голдстоун (вслед за Р. Ли) считал, что вековые циклы имеют экзогенный характер и как рост, так и уменьшение численности населения объясняется благоприятными или неблагоприятными изменениями климата[2]. П. Турчин[3] показал, что вековые циклы могут быть объяснены исходя из обычного мальтузианского постулата о том, что темпы роста населения увеличиваются при увеличении потребления и уменьшаются при его уменьшении. В простейшем случае, когда уровень потребления связан с популяционным ростом линейно, популяционная динамика математически описывается хорошо известным логистическим уравнением:

(1)

где N(t) - численность населения в момент t, r - естественный прирост в благоприятных условиях, К - емкость экологической ниши, то есть максимальная численность населения, которое может проживать на территории государства. Пусть S – параметр экономической государственной мощи, характеризующий те ресурсы, которые могут быть направлены на расширение экологической ниши путем увеличения продуктивности земель. К и S связаны соотношением

K = p - a+cS/(S+f)

где р – «естественная» емкость экологической ниши в отсутствие государства и внутренних войн, a – изъятие ресурсов в пользу государства (a<p), с и f - некоторые положительные константы. Поскольку S отражает состояние общества, то его можно трактовать также как параметр, характеризующий социополитическую стабильность. В простейшей модели, рассмотренной П. Турчиным («базовая фискально-демографическая модель»), предполагалось, что государство собирает налоги в виде части «избыточного продукта», т.е. совокупного продукта сверх того минимального уровня, который необходим для воспроизводства численности крестьян (но не его роста). В этой краткой заметке мы предлагаем модифицированную модель, в которой предполагается, что государство взимает часть не избыточного, а всего совокупного продукта, не взирая на то, хватит ли того, что остается крестьянам для простого воспроизводства их численности. То есть, в данной модели возможно состояние дел, при котором жесткая налоговая политика государства приводит к сокращению численности народа. Далее, в базовой фискально-демографической модели Турчина S не может быть отрицательным, то есть не учитывалась возможность крайней социополитической нестабильности, при которой внутренние беспорядки вызывают сокращение емкости экологической ниши ниже, чем ее естественный уровень. В данной модели учтена эта возможность. Мы будем полагать, что

(2)

где первое слагаемое соответствует государственным доходам, а второе – военным и полицейским расходам. dS/dt, таким образом, представляет собой приращение капитала, которое можно потратить на экономические нужды. В аграрных государствах налог обычно берется с пахотной площади, которая ограничена и, увеличиваясь с ростом населения, стремится к некоторой асимптоте, то есть изменяется примерно как N/(N+d) с некоторым коэффициентом a, характеризующим изъятие ресурсов в пользу государства; расходы при этом можно полагать пропорциональными численности населения.

Изменение структуры модели при переходе от базового к модифицированному варианту проиллюстрировано на рис. 1. В базовой фискально-демографической модели зависимость налоговых поступлений от численности населения принимает форму параболы, а расходы растут линейно. Когда население переходит точку N_крит, где эти кривые пересекаются, расходы начинают превышать доходы, государственная мощь начинает уменьшаться, что в конце концов приводит к краху государства. В случае модифицированной модели доходы продолжают увеличиваться асимптотически, но расходы все равно растут быстрее и со временем превосходят доходы. Возможен также промежуточный вариант поведения кривой доходов, этот случай будет обсужден позже.

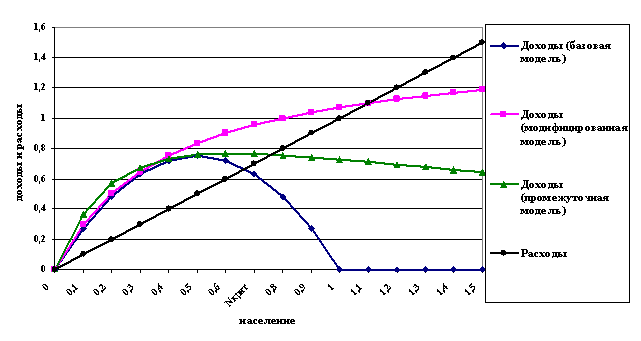
Рис. 1. Кривые доходов и расходов в различных вариантах фискально-демографической модели.

Таким образом, в модифицированной модели мы рассматриваем систему дифференциальных уравнений (1)-(2). Мы переобозначим коэффициенты в (2), введя параметр l = a/d. Этот параметр имеет реальный смысл, можно показать, что l – это душевая налоговая нагрузка при малой численности населения. Таким образом уравнение (2) принимает вид

(2a)

Можно показать, что фазовая плоскость (N, S) этой системы делится прямыми S = S₁= -(p-a)/(p-a+c)f и N=0 на четыре области (четверти), причем решения из верхней правой четверти G (которые только и имеют физический смысл) не пересекают указанные прямые, то есть всегда S> S₁, а так как S₁>-f, то знаменатель в формуле для К не обращается в ноль.

Система (1) – (2) имеет положение равновесия (N₀, S₀),

(3) N₀=a/b-a/l, S₀=(N₀- (p-a))f/(c+(p-a) - N₀)

Условия N₀>0, S₀>0 приводят к требованию

(4) N₁ = (p-a) < N₀< (p-a)+c = N₂

Обычные методы исследования динамических систем позволяют установить, что система (1)-(2) имеет характеристическое уравнение λ² +rλ +q = 0, где

(5) q = rN₀b²(N₂ - N₀)²/acf.

Дискриминант этого уравнения равен D = r²/4 – q. При этом возможны два случая.

1). Если q > r²/4, то D<0, характеристические числа комплексные и равны λ_1,2 = - r/2 ± i√(-D). Положение равновесия (N₀, S₀) в этом случае является так называемым «устойчивым фокусом» – вокруг этого положения равновесия происходят постепенно затухающие колебания (рис. 2 и рис. 3). Скорость уменьшения амплитуды колебаний пропорциональна exp(-rt/2), а период колебаний стремится к величине T = 2π/√ (-D), то есть с увеличением величины q период становится меньше, а амплитуда больше – колебания усиливаются.

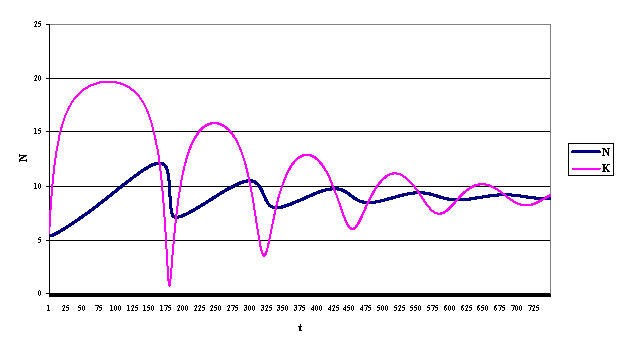
Рис. 2. Пример поведения решения в случае D<0 (r=0.01; p=10; a=3; b=0,3; l=3, c=17, f=15).

2). Если q < r²/4, то D>0. Так как в (5) N₀>0, то q >0 и D<r²/4, поэтому характеристические числа λ_1,2 = - r/2 ± √D отрицательны. Это значит, что положение равновесия – так называемый «устойчивый узел», решения стремятся к этому положению асимптотически, без колебаний.

Существование устойчивого равновесия, при котором население и мощь государства позитивны—новый тип динамического поведения, не наблюдаемый в базовой модели, в которой единственная возможная точка равновесия характеризуется отсутствием государства (S₀=0, N₀ = p-a).

Можно проанализировать влияние отдельных параметров на поведение системы. Если мы будем менять параметр l, то при уменьшении l величина N₀ , уменьшаясь, будет стремится к N₁, q будет возрастать и, следовательно, колебания будут усиливаться, а S₀ (как видно из (3)) будет стремится к 0. Это соответствует дестабилизации обстановки и уменьшению «равновесного» населения N₀ при уменьшении «равновесной» государственной мощи S₀. Когда S₀ близко к нулю, фазовые траектории в своей нижней части заходят в область S<0, что означает периодические внутренние войны и нестабильность (рис. 2). При дальнейшем уменьшении l N₀ становится меньше N₁, но остается пока положительным, в этом случае S₁<S₀< 0, то есть положение равновесия остается в области G, но S₀ отрицательно. Реально это означает, что равновесие теперь достигается в «безгосударственной» обстановке войн и смут. При приближении N₀ к нулю q также стремится к нулю, поэтому колебания постепенно стихают, а затем прекращаются. Положение равновесия (N₀, S₀) стремится к точке (0, S₁) и когда, с уменьшении l, N₀ становится равным 0, сливается с этой точкой. Фазовые траектории теперь асимптотически стремятся к этой точке, а N (t) асимптотически стремится к 0, то есть в случае, когда параметр l становится таким, что N₀ ≤ 0, население вымирает – происходит катастрофа.

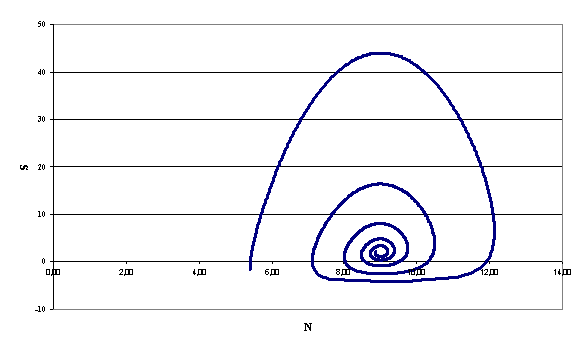
Рис. 3. Фазовая траектория (N(t), S(t)) (значения параметров те же, что и на рис. 1)

Если l возрастает, то N₀ также возрастет и (если a/b> N₂) стремится к N₂, при этом q (как видно из (5)) убывает и колебания ослабевают, а затем q становится меньше r²/4, и колебания прекращаются. S₀ при этом возрастает и, таким образом, повышение уровня «государственной мощи» S₀приводит к «успокоению» и росту «равновесного» населения N₀. Однако, если N₀ переходит границу N₂, то ситуация меняется: как видно из (3) S₀ становится большим отрицательным числом, и положение равновесия (N₀, S₀) исчезает из области G. В новой ситуации S(t) с течением времени неограниченно возрастает, а N(t) стремится к асимптоте N(t)= N₂. Таким образом, рост «государственной мощи» больше не приводит к существенному росту населения.

Параметр l характеризует душевую налоговую нагрузку (при малой плотности населения). Чем больше налоговая нагрузка, тем больше «государственная экономическая мощь». Слабость же государства оборачивается усилением нестабильности.

Параметр f характеризует скорость реакции экологической ниши на усиление или ослабление государства, чем больше f, тем слабее эта реакция. Изменение f не влияет на N₀, но, как видно из (3) и (5), увеличение f вызывает увеличение S₀ и уменьшение величины q, в этом случае колебания затухают и прекращаются. При уменьшении f колебания усиливаются, S₀ уменьшается (но остается положительным), при этом некоторые фазовые траектории заходят в область S<0, что означает внутренние войны. Таким образом, чем медленнее реагирует экологическая ниша на изменение S, тем стабильнее ситуация, и при очень слабой реакции колебаний не наблюдается.

Параметр с характеризует силу влияния государства на изменение экологической ниши, так же как f, он не влияет на N₀, но влияет на S₀и q. При увеличении с S₀уменьшается (но остается положительным), величина q возрастает и колебания усиливаются. При этом фазовые траектории в своей нижней части заходят в область S<0, что, как отмечалось выше, означает периодические внутренние войны (рис. 2). Такая ситуация, вероятно, была характерна для стран, в которых государство создавало и поддерживало крупные ирригационные системы, и где разрушение этих систем в результате ослабления государства приводило к голоду и гражданским войнам (например, для Китая).

Параметр b характеризует степень зависимости военных и полицейских расходов от численности населения. При увеличении b N₀ и S₀ уменьшаются, колебания усиливаются, и как описано выше, может произойти катастрофа. В истории известно много случаев, когда увеличение военных расходов приводило к социально-политическим кризисам, голоду и уменьшению численности населения. При уменьшении военных расходов N₀ и S₀ увеличиваются, но N₀ возрастает лишь до определенного предела N₂, после которого уменьшение военных расходов уже не приводит к росту населения.

Параметр а характеризует объем извлекаемых из населения ресурсов. При уменьшении а N₀ и S₀ уменьшаются, колебания усиливаются, а при дальнейшем сокращении налогов государство слабеет и может произойти катастрофа. При увеличении а N₀ и S₀ увеличиваются, однако одновременно уменьшается N₂, и очень скоро наступает момент, когда N₀ становится больше N₂ и рост налогов останавливает рост населения, которое стремится к асимптоте N(t)= N₂. При дальнейшем росте a асимптота N₂ понижается, то есть население сокращается.

Таким образом, исследование системы (1)-(2) показывает, что в демографически-структурной модели возможны как асимптотические решения, так и колебательные процессы – все зависит от конкретных параметров системы. Существенно, однако, что с течением времени и в отсутствие возмущений колебания успокаиваются. Как мы отметили выше, в базовой модели устойчивое равновесие между N и S>0 невозможно. Это равновесие возникает в модифицированной модели, потому что она предполагает, что способность государства изымать налоги не уменьшается, когда население достигает точки, где продукта не хватает на простое воспроизводство. Это упрощение реальности, ведь когда население голодает, вряд ли оно с готовностью отдаст часть своего урожая сборщикам налогов. Крестьяне будут скрывать зерно в тайниках (как происходило в Советской России во времена продразверсток), могут быть волнения и восстания, казна начинает не добирать налоги, и бывает вынуждена прощать недоимки (как происходило в Римской империи периода распада). С другой стороны, предположение базовой модели о том, что государство может собирать налоги только, когда имеется излишек, тоже серьезно упрощает реальность. Случаи, когда государство изымало налог несмотря на повсеместный голод вполне обычны в истории. Два варианта модели, однако, упрощают реальность «в противоположных направлениях», что позволяет нам определить рамки возможных вариантов поведений систем население-государство.

В этой связи представляет интерес также промежуточный вариант модели, когда по мере роста населения ухудшается собираемость налогов, но доходы все же не падают до нуля, а стремятся к некоторой асимптоте (см. рис. 1). В этом варианте уравнение (2) имеет вид

(2b)

где m – коэффициент, определяющий размеры «недоимки» (0<m<1). В случае промежуточной модели мы не можем дать строгое аналитическое описание ее поведения, такое, как для модифицированной модели. Однако расчеты показывают, что эти модели ведут себя, в целом, одинаково (при малых m это можно доказать теоретически). Расчеты показывают, что в случае, когда при m=0 (то есть в модифицированной модели) мы имеем положение равновесия типа «фокус», при увеличении m колебания усиливаются, а N₀ и S₀уменьшаются. В конце концов, с ростом m S₀становится отрицательным, но N₀ не стремится к 0, и положение равновесия сохраняет колебательный характер.

Различие между динамиками вариантов модели указывает, что коллапс государства можно избежать только в том случае, когда государство достаточно сильно и автономно от общества, а также готово применять жесткие меры для поддержания своего финансового здоровья. И все равно, достигнутое равновесие остается хрупким, так что сильные экзогенные воздействия могут изменить значения системных параметров и довести систему до коллапса.

Авторы выражают признательность профессору С. В. Цирелю за полезное обсуждение статьи.

Примечания